Heap
힙은 완전 이진트리를 활용하는 자료구조로 최대값과 최소값을 빠르게 구하기 위해 고안되었다
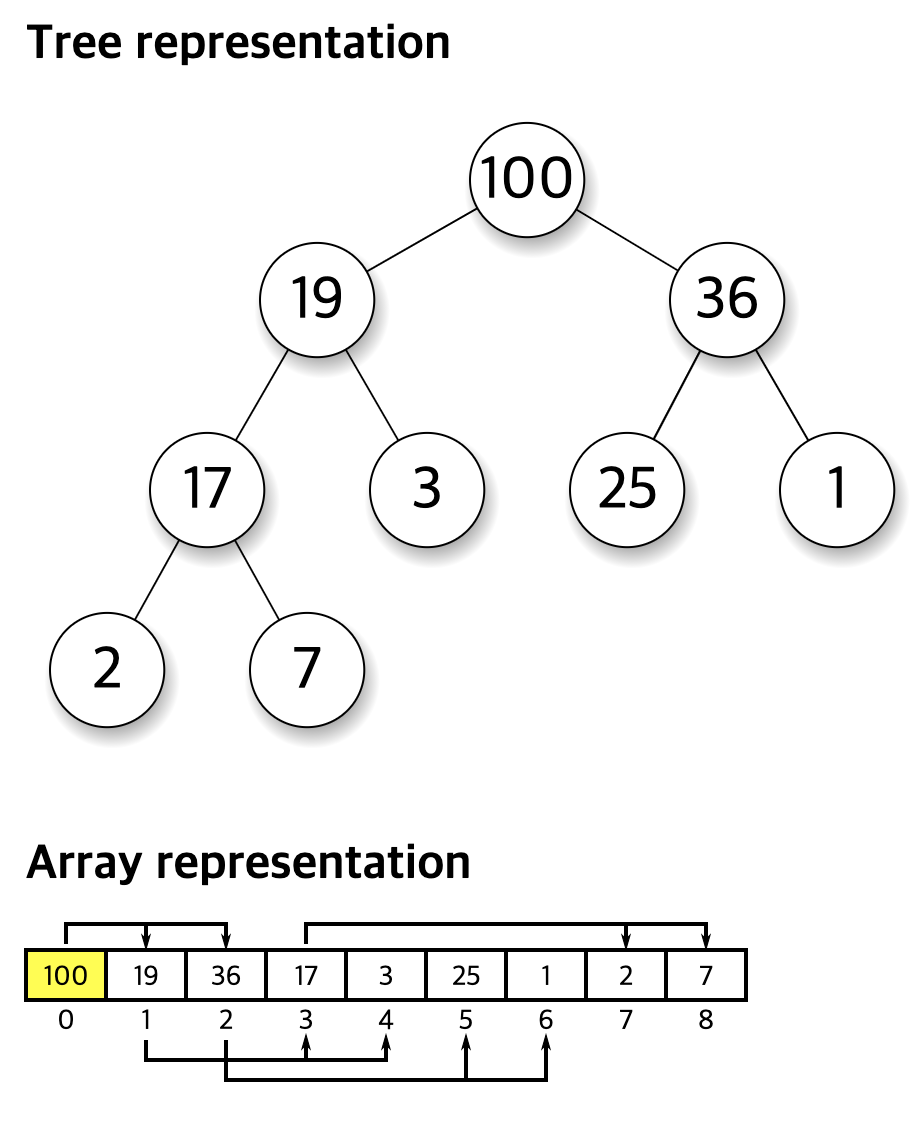
최대값이 root 노드가 되는 maxheap의 그림
보통 이진 트리로 표현되지만 아래의 그림처럼 배열로도 표현할 수 있으며 이 글에선 배열로 구현한 heap만 다룬다
삽입
heap의 끝 자리에 노드를 추가하고 자신의 부모와 비교해서 부모보다 크거나/작을 때 까지 부모와 위치를 바꾼다
삭제
heap의 루트 노드를 삭제한 뒤 heap의 제일 마지막 노드를 root로 옮긴 뒤 왼쪽과 오른쪽 자식들을 비교해서 크거나/작을 때 까지 자식과 위치를 바꾼다
코드
class Heap{
constructor(compare) {
this.arr = [];
this.compare = compare;
}
get size(){
return this.arr.length;
}
get array(){
return this.arr;
}
insert(elem){
this.arr.push(elem);
let child = this.size-1;
let parent = Math.floor((this.size-2)/2);
while (this.compare(this.arr[parent],this.arr[child])){
this.swap(parent,child);
child = parent;
parent = Math.floor((child-1)/2);
}
}
delete(){
if(this.size<2) {
return this.arr.pop();
}
const temp = this.arr[0];
this.arr[0] = this.arr.pop();
let parent = 0;
while ((parent*2+1) < this.size){
const left = parent*2+1;
const right = parent*2+2;
const target = right < this.size && this.compare(this.arr[left], this.arr[right])
? right : left;
if(this.compare(this.arr[left], this.arr[right])) break;
this.swap(parent, target);
parent = target;
}
return temp;
}
swap(a,b){
const temp = this.arr[a];
this.arr[a] = this.arr[b];
this.arr[b] = temp;
}
}callback으로 비교함수를 받아서 최대힙, 최소힙 두개를 다 생성할 수 있게 했다
'Algorithm > 개념' 카테고리의 다른 글
| 비트 마스크 (0) | 2021.05.16 |
|---|---|
| Graph (0) | 2021.04.25 |
| 2차원 배열 회전시키기 (0) | 2021.04.17 |
| Sort - 기본 (0) | 2020.12.18 |
| 에라토스테네스의 체 (0) | 2020.12.13 |
